최적 이진 탐색 트리 (Optimal Binary Search Tree)
이전 포스팅에서 설명했던 이진 탐색 트리 (BST) 의 활용 예를 보자. 설명할 때는 보통 이해하기 쉽게 노드에 들어있는 데이터를 숫자로 가정하지만, 실제로 쓰일 때는 문자열이라던가 더 다양한 데이터가 들어갈 수 있다. 예를 들어 주소록에서 어떤 사람 이름을 검색하기 위해 BST를 만들었다고 치자.
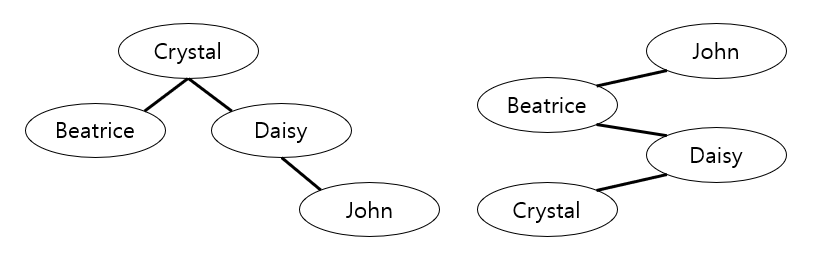
보면 알겠지만 여기서는 크다, 작다의 기준은 알파벳 ABC순 정렬이다. B로 시작하는 단어가 C로 시작하는 단어보다 왼쪽에 위치하게 되는 것이다.
서로 다른 모양의 트리 2개를 그려놨는데 둘 다 BST다. 그러니까 같은 데이터셋을 가지고 만들 수 있는 BST의 모양은 유일하지 않다. 이 두 BST의 차이는 무엇일까? BST에서 검색을 할 때는 루트 노드부터 시작해서 재귀함수를 호출하면서 아래로 내려가기 때문에, 검색할 대상이 아래쪽에 있을수록 함수 호출을 해야 하는 횟수가 늘어난다. 예를 들어 'Crystal' 을 검색한다고 하면 왼쪽 BST에서는 바로 결과가 나오지만 오른쪽 BST에서는 3번 더 내려가야 한다. 그렇다면 다른 제약사항이 없다고 했을 때 일반적으로 생각할 수 있는건 BST를 최대한 적은 층수 (레벨) 로 구성하는 게 좋다고 생각할 수 있다.
다만 현실에서는 여기에 제약사항이 더 붙는다. 이를테면 단어별로 검색 요청이 들어오는 빈도가 다른데, John은 영어에서 아주 흔한 이름이므로 검색 빈도가 높을 것이라고 생각할 수 있다. 단어별로 검색 빈도가 아래와 같다고 가정하자.
Crystal = 0.1 / Daisy = 0.2 / Beatrice = 0.3 / John = 0.4
BST의 '평균 검색 시간' 은 단어별 '검색 빈도 * 필요 탐색 횟수' 를 모두 더한 것이라고 정의한다. 식으로 표현하면 다음과 같다. c는 단어를 검색하는데 필요한 함수 호출 횟수, p는 단어의 검색 빈도, n은 단어의 수를 의미한다.
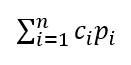
위 예시의 두 BST에 대해서 이걸 계산해보면,
왼쪽: (0.1*1) + (0.2*2) + (0.3*2) + (0.4*3) = 2.3
오른쪽: (0.1*4) + (0.2*3) + (0.3*2) + (0.4*1) = 2.0
으로 오른쪽 BST가 더 효율이 좋다는 것을 알 수 있다. 직관적으로 표현하면 검색 빈도가 높은 단어가 깊은 곳에 박혀있으면 효율이 떨어지고, 반대로 루트 노드와 가까운 곳에 있으면 효율이 좋다는 얘기다. 오른쪽 BST가 트리의 레벨은 1 더 높지만, 제일 검색 빈도가 낮은 Crystal을 아래로 내리고 검색 빈도가 높은 John을 루트 노드로 놓으니 오히려 효율이 더 좋아졌다.
가능한 BST의 모양들 중에서 평균 검색 시간이 제일 낮은, 가장 효율적인 트리를 최적 이진 탐색 트리 (Optimal BST) 라고 부른다. 그럼 단어들이 주어졌을 때 최적 BST를 어떻게 찾아낼까?
가능한 모든 BST의 모양을 만들어보는 건 너무 비효율적이다. 노드 n개가 있고 어떤 노드를 루트에 뒀을 때, 그 노드를 제외한 나머지 n-1개의 모든 노드들은 부모 노드의 왼쪽이나 오른쪽에 위치할 수 있으므로 가능한 BST의 경우의 수가 2^(n-1) 개이다. 즉 지수 시간복잡도라는 얘기다.
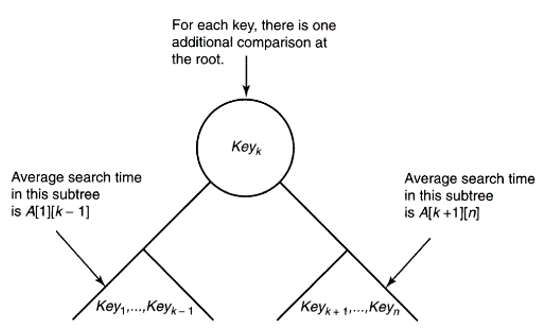
그래서 최적 BST를 빨리 찾기 위해서 또 다이나믹 프로그래밍이 등장한다. BST의 특성상 어떤 BST의 왼쪽, 오른쪽 서브트리가 각각 최적 BST여야 해당 BST도 최적이다. 즉 최적의 원리가 성립한다.
위 그림을 보자. 어떤 BST가 1번째 key (단어) 가 루트라는 제약사항을 가진 최적 BST라고 하자. 왼쪽, 오른쪽 서브트리는 각각 최적 BST이고, 전체 BST에서 단어를 찾을 때 걸리는 평균 검색 시간은 서브트리에서 찾는 시간 + 루트노드를 탐색하는 시간이다.
이걸 식으로 세워보자.
먼저 i번째 key부터 j번째 key까지로 최적 BST를 만들었을 때의 평균 검색 시간, 즉 최적값을 A[i][j] 라고 정의하자. 그러면 서브트리의 평균 검색 시간은 루트노드가 k번째 key일 때 왼쪽, 오른쪽 각각 A[1][k-1], A[k+1][n] 이다 (서브트리는 각각 최적 BST이므로). 그리고 루트노드는 깊이가 1이므로
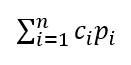
에서 c를 뺀 (c=1) 것이 루트노드를 탐색하는 시간이다.
그리고 k개의 BST 중 하나는 반드시 최적이다. 서브트리들은 이미 최적이라고 했기 때문에 루트노드를 k번 바꿔보고 그 중 최적의 값을 구하면 그게 전체에 대한 최적의 값이다. 이를 종합하면 아래와 같은 식이 나온다.

1부터 n까지가 아니라 i번째부터 j번째까지의 key로 일반화할 수도 있다. 그러면 아래와 같은 식이 된다.
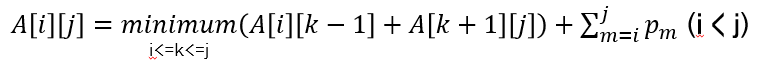
이 식을 이용해서 A라는 2차원 배열을 채워나가서, A[1][n] 의 값을 얻으면 그것이 최적 BST의 평균 검색 시간 (최적값) 이 된다.
다만 A라는 DP 배열 하나만으로는 최적값은 구할 수 있지만 최적 BST의 모양을 알 수가 없다. 최적 BST를 구성하기 위한 아이디어는 R이라는 2차원 배열을 하나 더 만드는 것이다. 여기서 R의 각 칸에 들어가는 값은 A 배열에 최적값을 넣는 순간의 k값으로, 이는 즉 i번째 key부터 j번째 key까지를 이용해 BST를 만들 때 루트가 되는 노드의 번호를 의미한다. 즉 R[1][n] 을 구하면 최적 BST의 루트노드를 구할 수 있다. 그 다음 레벨의 노드부터는? 루트가 된 노드가 k번 노드라고 치면 그 왼쪽 서브트리의 루트노드 (즉 k번 노드의 left child) 는 R[1][k-1], 오른쪽 서브트리의 루트노드는 R[k+1][n] 이 된다. 이런 식으로 R 배열의 값들을 이용해 재귀함수를 호출해주면서 노드를 만들어나가면 최적 BST가 만들어진다.

예시를 보면서 이해해보자. 4개의 key (단어) 들이 있고 각각의 검색 빈도는 왼쪽과 같다. A 배열이든 R 배열이든 'i번째부터 j번째 key를 이용해서 만든 최적 BST' 에 대한 내용을 담고 있으므로, i<=j인 경우만 생각하면 된다. 그러므로 대각선을 기준으로 왼쪽 아래에는 값을 넣을 필요가 없고, 대각선 칸은 0으로 모두 채운다.
i=j인 경우는 하나의 단어, 그러니까 노드 하나뿐인 BST가 되므로 A 배열에는 그 단어의 검색 빈도가 그대로 들어가고 R 배열에는 그 단어의 번호가 들어간다.
그 다음 칸부터 본격적으로 위의 점화식을 이용해서 칸을 채운다. 예를 들어 A[1][2] 의 경우,
A[1][0] + A[2][2] (k=1인 경우)
A[1][1] + A[3][2] (k=2인 경우)
둘 중에 작은 값을 선택하게 되는데 둘 다 3/8이고, 거기에 각 key의 검색 빈도를 다 더하므로 3/8이 두번 더 더해져서 9/8이 된다. R[1][2] 에는 선택한 작은 값에 해당하는 k값을 넣는데 여기서는 1, 2를 둘 다 넣을 수 있지만 동률일 경우 더 작은 값을 우선으로 넣기로 한다.

A, R 배열을 만드는 파이썬 함수를 작성했다. 신경쓰일 만한 부분은 주석으로도 달아놨지만 한번 더 써보면,
- n은 key의 개수, p는 각 key에 대한 검색 빈도가 저장되어 있는 리스트다.
- 아까 위에서 봤던 예시 그림에서 A, R 배열을 잘 보면 가로로는 0, 1, 2... 인데 세로로는 1, 2, 3... 이다. 그러니까 코드를 좀 더 이해하기 쉽게 작성하기 위해서 세로로 한 줄을 더 만들었다. 위 그림이랑 비교해서 제일 위에 0으로 채워진 한 줄이 더 있는 것이다. 메모리 낭비라고 생각할 수 있지만 예시니까 넘어가자
- for문 두 개와 diagonal 변수는 대각선 기준으로 위쪽만 돌기 위해 저렇게 만들었다.
- 그 아래로는 점화식을 코드로 옮긴 것이다. 첫번째 for문은 minimum 찾는 부분, 두번째 for문은 p값들을 더하는 시그마 부분이다.

위에서 만든 R 리스트를 이용해서 최적 BST를 만드는 함수다. 아까 R 배열에 대해서 설명할 때 언급했듯 재귀적으로 동작하므로 i, j를 인자로 받아야 한다. 예시처럼 key가 4개라면, 처음 호출할 때는 (1, 4, R, Keys) 로 호출하면 된다. Keys는 말 그대로 key 단어들이 들어가있는 리스트다.
R 리스트에서 k를 가져온 다음, k가 0이 아니라면 k번째 key를 사용해서 노드를 만든다. 그리고 이 노드의 왼쪽, 오른쪽 자식노드를 각각 재귀호출로 만든다. 마지막에 return node를 해줘야 만들어진 노드 객체가 부모 노드의 left, right 속성으로 들어간다는 점을 주의하자.