AOV/AOE Network를 이용한 작업 시간 구하기
얼마 전에 우연한 계기로 어떤 알고리즘 문제를 풀게 됐는데, 딱 보자마자 학부 시절 자료구조 시간에 배웠던 AOE Network와 Critical Path라는 개념이 떠올랐다. 그걸 이용해서 문제를 풀 수 있겠다는 생각은 들었지만, 문제는 그 개념만 떠올랐지 어떻게 구현하는지는 하나도 기억이 안났다. (...) 결국 제대로 풀지 못했다.
그래서 이번 포스팅에서는 AOV Network, AOE Network (둘은 비슷한 개념이다) 의 개념과 구현 방법에 대해 정리해 본다. 포스팅을 쓰기 위해서 옛날 그 학부 시절에 짰던 코드를 예토전생시켰는데, 날짜를 보니까 거의 6년이 됐더라. 까먹을 만도 하다... 그 코드를 봐도 하나도 이해가 안돼서 인터넷에서 강의자료를 찾아보면서 아예 다시 공부를 했다.
1) AOV Network / AOE Network란?
'스타크래프트' 같은 전략 시뮬레이션 게임을 예로 들어보자. 이런 게임을 해보면 대체로 테크트리라는 개념이 있어서, 처음부터 모든 건물을 지을 수 없다. 강력한 유닛을 뽑을 수 있게 해주는 고급 건물을 지으려면 다른 건물을 이미 지은 상태여야 한다는 제약조건이 있다.
예를 들어서 스타크래프트의 프로토스라는 종족의 건물 테크트리를 보자.

'게이트웨이' 를 지으려면 '넥서스' 가 필요하고, '사이버네틱스 코어' 를 지으려면 '게이트웨이' 가 필요하다는 식이다.
이 때, 가장 아래쪽에 있는 최종 건물인 '아비터 트리뷰널' 을 지으려면 시간이 얼마나 걸릴까? 라는 생각을 해볼 수 있다. '아비터 트리뷰널' 부터 시작해서 위로 쭉 훑어보면서 어떤 건물들이 필요한지 확인해 보자. 넥서스 - 게이트웨이 - 사이버네틱스 코어까지는 공통적으로 필요하고, 시타델 오브 아둔이랑 템플러 아카이브, 스타게이트까지 지어야 한다는 것을 알 수 있다. 이 각각의 건물들을 짓는데 걸리는 시간은 다음과 같다.
| 건물 이름 | 넥서스 | 게이트웨이 | 사이버네틱스 코어 | 시타델 오브 아둔 | 템플러 아카이브 | 스타게이트 | 아비터 트리뷰널 |
| 시간 (s) | 120 | 60 | 60 | 60 | 60 | 70 | 60 |
단순히 이 숫자들을 다 더하면 그게 답일까? 아니다. 테크트리를 잘 보면 '시타델 오브 아둔 - 템플러 아카이브' 테크랑 '스타게이트' 테크는 서로 의존성이 없다는 것을 알 수 있다. 건물을 짓는데 필요한 자원과 일꾼이 충분하다고 가정하면, '시타델 오브 아둔' 이랑 '스타게이트' 는 동시에 건설을 시작할 수 있다.
그러면 전자랑 후자 중에 어느 쪽이 더 오래 걸리는지만 고려하면 된다. 전자의 건물 두 개를 짓는데는 120초, 스타게이트를 짓는데는 70초가 걸리므로 양쪽을 다 갖추는 데는 결국 120초가 필요한 것이다. 결론적으로 아비터 트리뷰널을 짓는데 걸리는 총 시간은 다음과 같다.
120 + 60 + 60 + (60 + 60) + 60 = 420초
(* 실제 게임에서는 넥서스는 기본적으로 주어지고, 프로토스 종족의 특성상 넥서스 외의 건물을 짓기 위해서는 파일런이라는 건물도 지어줘야 하지만 위 그림에는 나타나있지 않고 이 글이 스타 강좌는 아니므로 고려하지 않기로 한다)
이러한 개념을 일반화한 것이 AOV (Activity-On-Vertex) Network이다. Vertex (정점) 와 Edge (간선) 들로 구성된 그래프가 있고, 그래프의 각 Vertex들은 방향성을 가지고 연결되어 있다. 여기서 Vertex는 작업을 의미하며, 각 Vertex에는 작업을 수행하는데 걸리는 시간이 Weight 값으로 부여되어 있을 수 있다 (없는 경우도 있다). 예를 들면 아래 그림과 같다.

이런 형태가 주어졌을 때, 'F라는 작업을 하기 위해서는 미리 어떤 작업들을 끝내놔야 하는가?' 혹은 'F라는 작업을 끝내기 위한 최단 시간은 얼마인가?' 와 같은 문제를 풀기 위해 고안된 자료구조이다.
Vertex 대신에 Edge에 Weight를 부여하면 AOE (Activity-On-Edge) 네트워크라고 부른다. AOV 네트워크랑 대충 비슷하지만, AOE 네트워크에서는 Edge가 작업을 의미하고 Vertex는 작업을 끝낸 '상태' 를 의미하게 된다. 또는 '사건' (Event) 이라 부르기도 하는데, '사건' 이 발생하려면 그 Vertex의 앞에 연결된 모든 작업들이 완료되어야 하며, '사건' 이 발생하지 않으면 그 Vertex의 뒤에 연결된 어떤 작업도 시작될 수 없다.
모든 작업이 일직선적으로 Dependency를 가지고 있거나, 작업을 수행할 수 있는 자원이 한정적이라서 (ex: 일할 사람이 한명밖에 없는 경우) 한번에 하나의 작업밖에 수행할 수 없는 경우엔 필요가 없고, 병렬적으로 작업이 수행될 수 있는 경우에 사용된다.
이러한 AOV/AOE 네트워크는, 위에서는 게임에서의 건물 건설을 예로 들었지만 실제로도 건축이나 생산 공정, 혹은 회사에서 프로젝트 진행에 대한 계획을 짤 때 등등 산업공학 분야에서 곧잘 응용되는 개념이라 한다.
2) 작업 순서 구하기: 위상 정렬 (Topological Sort)
먼저 기본적인 문제부터 살펴보자. Weight가 없는 AOV 네트워크, 그러니까 작업들간의 Dependency만 정의되어 있는 그래프라고 하자.
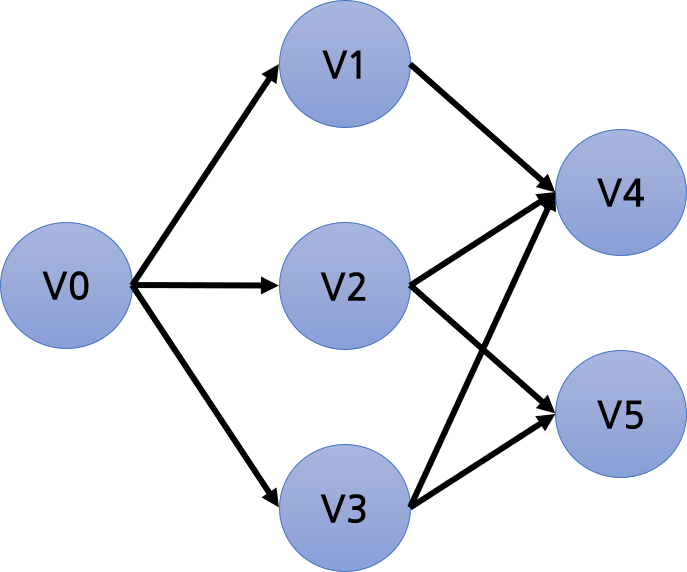
문제는 이 그래프에서 Dependency 관계를 고려해서, 작업을 어떤 순서로 처리해야 하는지를 알아내는 것이다. 예를 들면 V5를 V2보다 먼저 할 수는 없다 (이 그림은 단순하게 생겨서 딱 봐도 그 사실을 알 수 있지만 더 복잡하다고 생각해보자).
이러한 문제를 해결하는 알고리즘을 위상 정렬 (Topological Sort) 이라고 한다. 보통 프로그래밍에서 정렬이라고 하면 숫자나 문자열 같은걸 정렬하는 걸 많이 떠올리겠지만 여기서는 그래프의 Vertex를 정렬하는 것이다. 어떤 순서로? 먼저 처리해야 하는 일부터.
- 그래프를 표현하기 위한 자료구조: 인접 리스트 (Adjacency List)
보통 그래프를 표현할 때 많이 쓰는 자료구조로 인접 행렬 (Adjacency Matrix) 이 있는데, AOV/AOE 네트워크 문제를 풀 때는 인접 행렬보다 인접 리스트라는 것을 많이 사용한다. 인접 리스트는 각 Vertex간의 연결 관계를 Linked List로 만든 것이다. 예를 들면 위 그림의 그래프를 인접 리스트로 만들면 아래와 같다.
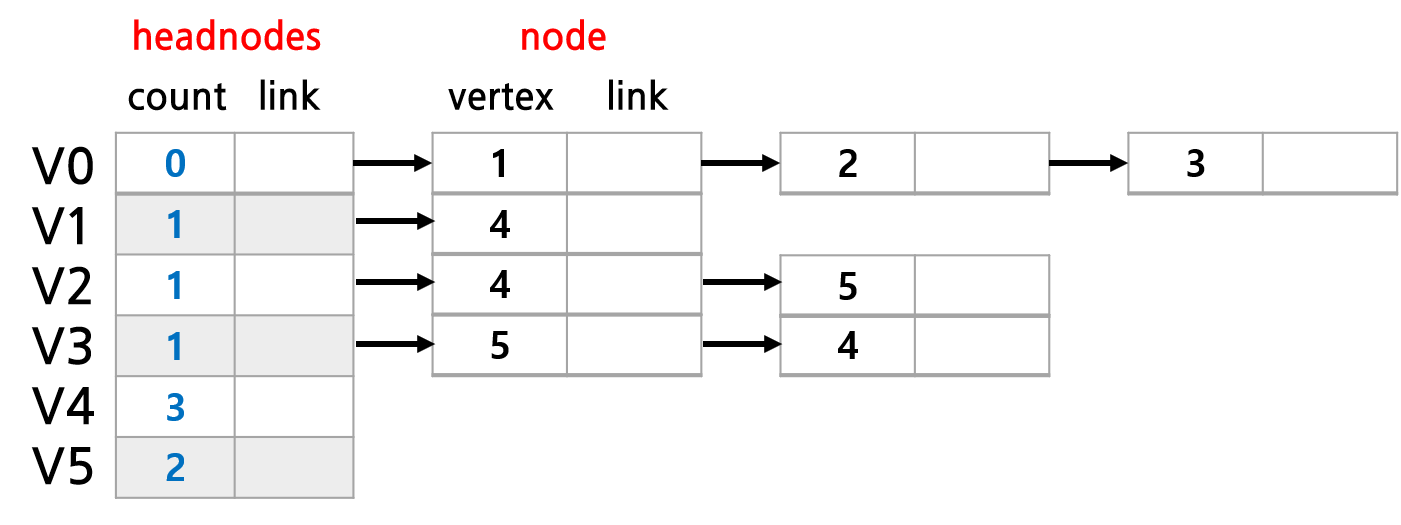
count란 해당 Vertex로 들어오는 Edge의 개수 (in-degree) 를 의미한다. 예를 들어 V4는 V1, V2, V3으로부터 화살표를 받고 있으므로 count가 3인 것이다. link는 해당 Vertex에서 나가는 Edge와 연결된 노드들을 가리킨다. V2의 경우 V4, V5로 뻗어나가므로 link와 4, 5가 연달아 연결되어 있다.
C-style로 이러한 자료구조를 표현하면 아래와 같다 (나는 요즘 C를 잘 안쓰지만 공부하다보니 다들 참고하는 책에 이렇게 써 있어서...).
typedef struct node *node_pointer;
typedef struct node{
int vertex;
node_pointer link;
};
typedef struct{
int count;
node_pointer link;
} hdnodes;
hdnodes graph[MAX_VERTICES];
- 위상 정렬 알고리즘: 스택을 이용한 DFS
위에서 인접 리스트를 이용해서 그래프를 표현했는데, 이 그래프를 가지고 이제 위상 정렬을 해야 한다. 알고리즘은 다음과 같다.
- count가 0인 Vertex들을 Stack에 넣는다
Stack이 빌 때까지 아래를 반복한다:
- Stack에서 Vertex 하나를 꺼낸다
- 해당 Vertex가 가리키는 다른 Vertex들에 대하여 count를 1씩 감소시킨다
- count가 0이 된 Vertex가 있으면, Stack에 넣는다
정렬 결과는 Stack에서 pop된 순서와 같다.
직관적으로 이해하기 좀 어려운 것 같기도 한데, count 값이 남아있다는 것은 아직 그 Vertex 이전에 거쳐야 하는 Vertex가 있다는 뜻이므로 count가 남아있는 작업은 아직 시작할 수가 없다. 반대로 count가 0이면 그 Vertex 이전에 거쳐야 하는 Vertex들을 이미 모두 거쳐왔거나 그런 Vertex가 없다는 뜻이므로 바로 시작할 수 있는 작업이라는 소리다.
위 그래프의 예시를 가지고 이 알고리즘이 실행되는 과정을 그림으로 살펴보자.




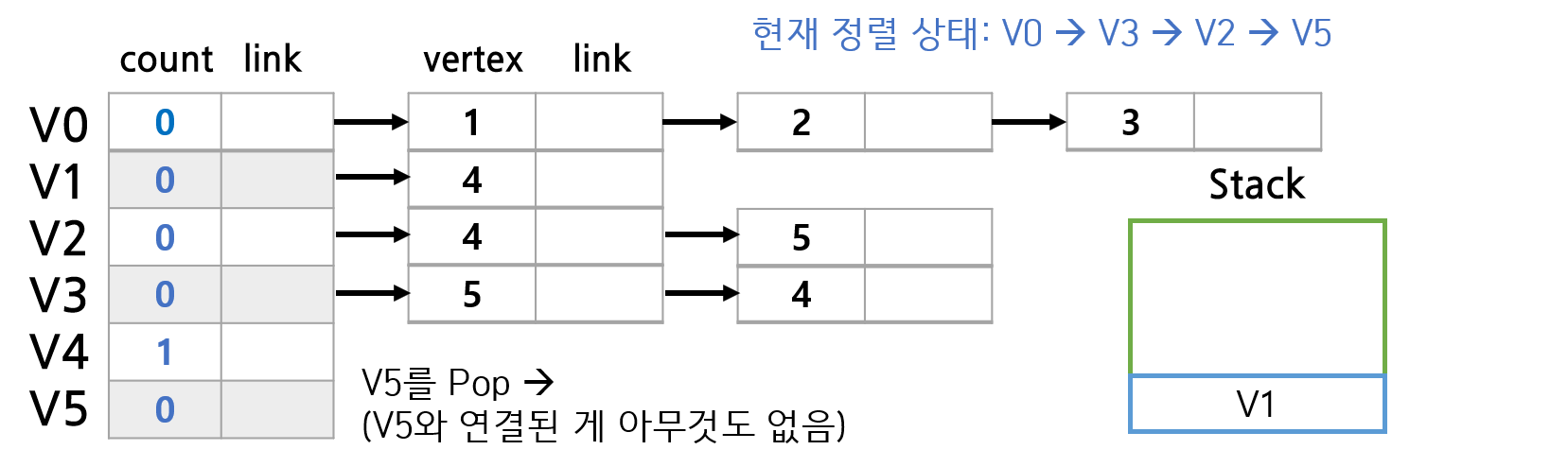


코드는 파이썬으로 이렇게 짰다. 파이썬에서는 굳이 링크드 리스트를 만들지 않아도 dict랑 set을 이용해서 해결이 가능했다. 스택 역시 따로 구현할 필요가 없이 그냥 list를 바로 스택처럼 쓸 수 있다.
graph = {0: set([1, 2, 3]),
1: set([4]),
2: set([4, 5]),
3: set([5, 4]),
4: set([]),
5: set([])};
graph_count = [0, 1, 1, 1, 3, 2];
stack = [];
sorted_arr = [];
for i in range(0, len(graph_count)):
if graph_count[i] == 0: # 최초에 count가 0인 Vertex들을 스택에 넣는 부분
stack.append(i);
while (len(stack) > 0):
print(stack);
v = stack.pop();
sorted_arr.append(v);
next_v = graph[v];
for i in next_v:
graph_count[i] = graph_count[i] - 1;
if graph_count[i] == 0:
stack.append(i);
print(sorted_arr);
BOJ 2252번 문제가 이 위상정렬을 이용하는 기본적인 문제다. 아래는 BOJ 2252번을 푼 코드이다.
N, M = input().split();
N = int(N);
M = int(M);
graph_count = [0 for i in range(0, N)];
graph = {}
for i in range(N):
graph[i+1] = set([]);
for i in range(M):
A, B = input().split();
A = int(A);
B = int(B);
graph[A].add(B);
graph_count[B-1] = graph_count[B-1]+1;
stack = [];
sorted_arr = [];
for i in range(0, len(graph_count)):
if graph_count[i] == 0:
stack.append(i+1);
while (len(stack) > 0):
v = stack.pop();
sorted_arr.append(v);
next_v = graph[v];
for i in next_v:
graph_count[i-1] = graph_count[i-1] - 1;
if graph_count[i-1] == 0:
stack.append(i);
for v in sorted_arr:
print(v, end=" ");
3) Weight가 존재하는 AOV 네트워크
(이 영상의 도움을 많이 받았다. 참고!)
작업을 해야하는 순서 뿐 아니라, 각 작업들을 끝내는데 필요한 시간을 알고 있을 때 모든 작업을 끝낼 수 있는 최단시간을 구하는 문제를 풀고 싶다. 위 그림과 같이 각 Vertex에 그 작업을 끝내는데 걸리는 시간이 Weight 값으로 주어져있다고 하자.
먼저 다음과 같은 용어들을 정의하고 시작한다.
- EST (Earliest Start Time): Vertex에 해당하는 작업을 시작할 수 있는 가장 빠른 시간을 뜻한다.
ex) V3가 활성화되려면 V0을 끝내야 하고, 그렇게 되기까지 7초가 걸리므로 EST(V3) = 7.
- LST (Latest Start Time): Vertex에 해당하는 작업을 이때부터 시작해도 이후의 작업을 지연시키지 않는 가장 늦은 시간을 뜻한다.
ex) V5를 활성화시키려면 V2와 V3을 끝내야 한다. 근데 V2는 10초가 걸리지만 V3은 8초가 걸리므로 V3은 V0이 끝나고 2초정도 놀다가 시작해도 V5를 제때 시작하는데 아무 문제가 없다. 따라서 LST(V3) = 7+2 = 9.
ex) 위의 스타크래프트 예시에서, '스타게이트' 는 '시타델 오브 아둔' 을 건설 시작한 뒤 50초 지나서 건설해도 '아비터 트리뷰널' 을 제때 짓는데 문제가 없다는 것을 떠올리자.
- Critical Activity: LST - EST = 0인 Vertex를 뜻한다.
- Critical Path: Critical Activity들만으로 이어진 경로를 뜻한다.
ex) V3의 경우 LST - EST = 2이므로 Critical Activity가 아니다.
V2는 EST = 7이고 LST도 7이므로 (V2는 바로 시작하지 않으면 V5가 지연될 것이다) Critical Activity이다.
Critical Path는 시작 Vertex부터 최종 Vertex까지의 가장 긴 경로의 길이이며, Critical Path의 소요시간이 곧 전체 작업이 다 끝나는데 필요한 최소 시간이 된다. '가장 긴' 이라는 단어랑 '최소 시간' 이라는 단어 때문에 헷갈릴 수도 있는데, 예를 들어서 조별과제를 하는데 나머지 사람들은 다 진작 자기 파트를 끝냈지만 1명이 마지막 날에서야 자기 파트를 완성했다면 제출은 그 사람에 맞춰서 마지막 날에 할 수밖에 없다는 얘기랑 같다.
Critical Path를 찾는 이유는 무엇일까? Critical하지 않은 작업들은 여유 시간이 있다는 뜻이고 Critical한 작업들은 그렇지 않다는 뜻이다. 그러므로 여유 인력이 남는다면 Critical한 작업들에 배치하면 전체 작업 시간을 줄일 수 있다.
그럼 각 Vertex의 EST랑 LST를 찾는 과정을 보자. 그림의 각 Vertex 밑에 있는 사각형 두 칸이 각각 왼쪽은 EST, 오른쪽은 LST를 의미한다.
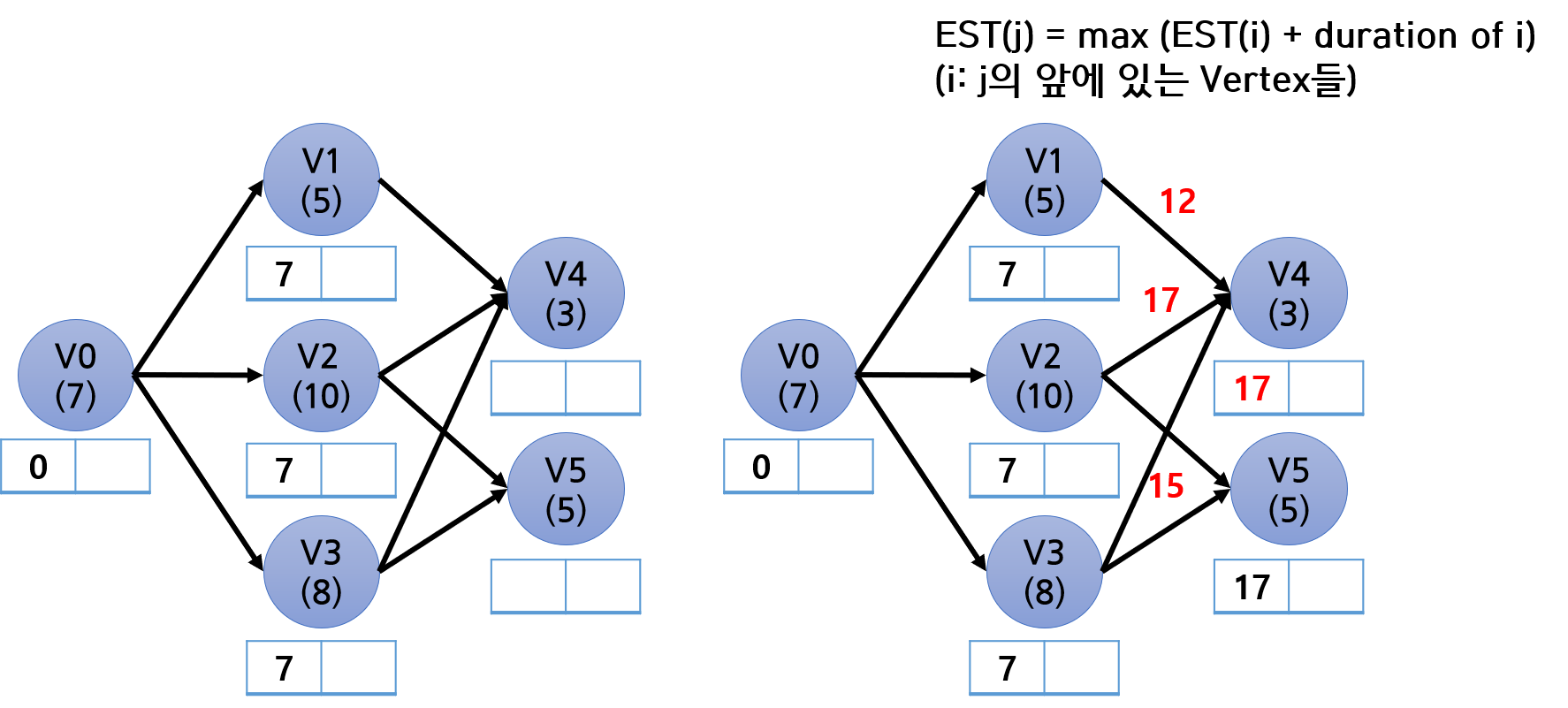
EST를 구할 때는 앞에서부터 뒤로 (즉, 위상 정렬 순서대로) 구한다.
기본적으로 [다음 Vertex의 EST = 이전 Vertex의 EST + 이전 Vertex의 duration] 이다.
V0을 처리하는데 7초가 걸리므로 V1, V2, V3은 모두 빨라야 7초 시점에서 시작할 수 있다. V1, V2, V3의 EST가 모두 7이라는 것은 쉽게 알 수 있다.
(* duration = 걸리는 시간. 위에선 weight라고 했는데, AOV/AOE 네트워크에서는 duration이란 용어를 많이 쓰더라)
V4, V5처럼 여러 Vertex가 앞에 연결되어 있는 경우에는 위 그림의 우상단에 써있듯, 각 선행 Vertex들에 대하여 위 계산을 한 값들 중에 max값을 취한다. 앞의 작업들이 다 끝나야 V4를 시작할 수 있으므로, V4의 시작 시간은 앞의 작업들 중 가장 늦게 끝나는 것에 의존하기 때문이다.

LST는 끝에서부터 시작해서 역방향으로 가면서, 위와 반대로 한다.
[이전 Vertex의 LST = 뒤 Vertex의 LST - 이전 Vertex의 duration] 이 되며, 여러개의 Edge가 모일 때는 min값을 취한다.
값들을 다 채워넣고 나니 EST와 LST의 값이 같은 Vertex들이 보인다. V0, V2, V4, V5가 Critical Activity이며, Critical Path는 [V0-V2-V4] 또는 [V0-V2-V5] 가 된다.
- 구현 (Python)
> 위 그림처럼 각 Vertex 객체에 EST, LST를 저장하는 필드를 추가한다. 또는 각 Vertex의 EST, LST 값들을 저장할 배열 (리스트) 을 따로 만든다.
> Topological Sort를 할 때 각 Vertex의 EST를 계산하는 다음과 같은 코드를 추가한다.
for i in next_v:
... # 이전의 그 코드
if EST[i] < EST[v] + duration[v]: # 더 큰값이 들어오게 되면, 갱신
EST[i] = EST[v] + duration[v];
EST 리스트는 다 0으로 초기화해둔다. 그러면 일단 계산된 값이 한번 들어가고, 더 큰 값이 새로 들어오게 되면 갱신할 것이다.
> LST를 구하기 위해서는 끝에서부터 시작해야 하기 때문에 Topological Sort의 반대 방향으로 돌아야 한다. 어떻게 할까? Topsort(inverse=true) 같은걸 끼얹나?
역 인접 리스트 (Inverse-Adjacency List) 를 이용하면 만들어 둔 위상정렬 알고리즘을 그대로 써서 반대 방향으로 정렬할 수 있다. 역 인접 리스트란 말 그대로 인접 리스트의 반대, 즉 그래프의 선 방향이 반대라고 치고 인접 리스트를 만든 것이다.
인접 리스트를 역 인접 리스트로 변환하기 위한 코드가 필요한데 이런 식으로 할 수 있다. 혹은, 입력을 인접 행렬 형태로 받는다고 하면 인접 행렬의 전치 행렬 (Transpose) 을 구한 다음 그걸 인접 리스트로 변환하는 방법도 있다.
for i in range(0, len(graph_count)):
nodes = graph[i];
for n in nodes:
inv_graph_count[i] = inv_graph_count[i]+1;
inv_graph[n].add(i);
> 최종적으로 이 프로그램이 돌아가는 과정은 다음과 같다.
- 인접 리스트를 만든다.
- 만든 인접 리스트를 기반으로 역인접 리스트를 만든다.
- 인접 리스트를 이용해 위상정렬을 하면서 EST들을 구한다.
- 가장 마지막 Vertex의 EST 값은 해당 Vertex의 LST 값으로 대입시켜 준다.
- 역인접 리스트를 이용해 위상정렬을 하면서 LST들을 구한다.
- 각 Vertex들에 대해 (LST - EST) = 0인지 여부를 검사하여 Critical Path를 출력한다.
아래는 예시 파이썬 코드이다. 중복되는 코드는 topsort() 함수로 묶는 등 약간 수정을 했다.
def topsort(graph, duration, graph_count, ST, direction):
stack = [];
sorted_arr = [];
for i in range(0, len(graph_count)):
if graph_count[i] == 0:
stack.append(i);
while (len(stack) > 0):
v = stack.pop();
sorted_arr.append(v);
next_v = graph[v];
for i in next_v:
graph_count[i] = graph_count[i] - 1;
if graph_count[i] == 0:
stack.append(i);
# EST를 구할 때는 direction=1, LST를 구할 때는 direction=-1을 주기로 한다
if direction > 0:
if ST[i] < ST[v] + duration[v]:
ST[i] = ST[v] + duration[v];
else:
if ST[i] > ST[v] - duration[i]:
ST[i] = ST[v] - duration[i];
return sorted_arr, ST;
VERTICES = 6;
graph = {0: set([1, 2, 3]),
1: set([4]),
2: set([4, 5]),
3: set([5, 4]),
4: set([]),
5: set([])};
inv_graph = {}
graph_count = [0, 1, 1, 1, 3, 2];
inv_graph_count = [0 for i in range(VERTICES)];
duration = [7, 5, 10, 8, 3, 5];
EST = [0 for i in range(VERTICES)];
LST = [99999 for i in range(VERTICES)];
for i in range(VERTICES):
inv_graph[i] = set([]);
# 인접리스트 -> 역인접리스트로 변환하는 부분
for i in range(VERTICES):
nodes = graph[i];
for n in nodes:
inv_graph_count[i] = inv_graph_count[i]+1;
inv_graph[n].add(i);
sorted_arr, EST = topsort(graph, duration, graph_count, EST, 1);
# 마지막 노드들은 LST = EST로 맞춰준다. 이 그래프는 마지막 노드가 2개라서 이렇게 해줬는데
# 다른 그래프면 또 달라져야 할 코드...
LST[VERTICES-1] = EST[VERTICES-1];
LST[VERTICES-2] = EST[VERTICES-2];
#
sorted_arr, LST = topsort(inv_graph, duration, inv_graph_count, LST, -1);
for i in range(VERTICES):
if EST[i] == LST[i]:
print("Vertex " + str(i) + " is Critical Activity");
4) AOE 네트워크
AOV 네트워크와의 차이점은 Edge에 Weight가 붙는다는 점이다. 위상 정렬이라던지 EST, LST같은 다른 개념은 다 똑같은데, 다만 자료구조를 만들 때 Vertex 대신 Edge에 Weight (duration) 값을 저장해줘야 한다는 점이랑 EST, LST 구할 때 Edge에 붙어있는 그 값을 쓴다는 점만 다르다.
아래 그림은 AOE 네트워크를 인접 리스트로 만든 것이다. headnodes가 아니라 그 뒤에 붙어있는 node들에 duration 값이 추가로 붙어있는 것을 볼 수 있다.

아래는 파이썬으로 구현한 코드이다. 위의 AOV 네트워크에서는 duration 값들이 Vertex 수만큼 있으면 됐기 때문에 그냥 따로 리스트로 만들었지만 AOE 네트워크에선 Vertex랑 Edge가 별개이기 때문에 graph를 2차원 dict 구조로 만들었고 그에 맞춰 코드를 수정했다.
def topsort(graph, graph_count, ST, direction):
stack = [];
sorted_arr = [];
for i in range(0, len(graph_count)):
if graph_count[i] == 0:
stack.append(i);
while (len(stack) > 0):
v = stack.pop();
sorted_arr.append(v);
next_v = graph[v];
for i in next_v:
graph_count[i] = graph_count[i] - 1;
if graph_count[i] == 0:
stack.append(i);
if direction > 0:
if ST[i] < ST[v] + graph[v][i]: # 기존의 duration 대신 graph에 접근
ST[i] = ST[v] + graph[v][i];
else:
if ST[i] > ST[v] - graph[v][i]:
ST[i] = ST[v] - graph[v][i];
return sorted_arr, ST;
VERTICES = 9;
# 2차원 dictionary 구조
graph = {0: {1: 6, 2: 4, 3: 5},
1: {4: 1},
2: {4: 1},
3: {5: 2},
4: {6: 9, 7: 7},
5: {7: 4},
6: {8: 2},
7: {8: 4},
8: {}};
inv_graph = {}
graph_count = [0, 1, 1, 1, 2, 1, 1, 2, 2];
inv_graph_count = [0 for i in range(VERTICES)];
EST = [0 for i in range(VERTICES)];
LST = [99999 for i in range(VERTICES)];
for i in range(VERTICES):
inv_graph[i] = {};
for i in range(VERTICES):
nodes = graph[i];
for n in nodes: # dict를 for-in으로 돌면? n은 안쪽 dict의 key들
dur = graph[i][n]; # 2차원 dict의 가장 안쪽에서 duration 값을 빼온다
new_dict = {}; # 기존 dict 안에 새로 넣을게 dict라고 정해주기 위함
new_dict[i] = dur;
inv_graph_count[i] = inv_graph_count[i]+1;
inv_graph[n].update(new_dict); # update가 아니라 대입을 하면 기존에 있던 값이 날아간다는 점 주의
sorted_arr, EST = topsort(graph, graph_count, EST, 1);
###
LST[VERTICES-1] = EST[VERTICES-1];
###
sorted_arr, LST = topsort(inv_graph, inv_graph_count, LST, -1);
for i in range(VERTICES):
if EST[i] == LST[i]:
print("Vertex " + str(i) + " is Critical Activity");
EST와 LST까지 같이 출력해본 결과. Critical Activity들을 잘 찾아냈다.