머신 러닝: Decision Tree 분류 알고리즘
요즘 컴퓨터공학 분야에서 가장 뜨거운 키워드를 꼽아보라면 머신 러닝 (기계 학습, Machine Learning) 을 빼놓을 수 없다. 인공지능 연구는 한때 이 분야는 더 이상 가망이 없다 endgame 며 지지부진하기도 했지만, 2000년대 이후로 다시 슬금슬금 뜨다가 구글이 집중적으로 이 분야를 파면서 다시 활기를 얻은 느낌이다. 특히 국내에서는 딥마인드 챌린지 매치 (알파고 vs 이세돌) 이후로 폭발적으로 관심이 늘었다. 그때가 내가 대학원을 다니던 시기였는데, 내가 졸업할 때쯤에는 다른 연구실은 다 파리날리는데 AI 다루는 랩들에만 신입생이 가득 차는 광경을 볼 수 있었다.
여튼 이 포스팅에서는 흔히 '머신 러닝' 으로 불리는 기술의 기본 개념과 널리 쓰이는 분류 알고리즘, 그리고 분류 알고리즘 중에서도 가장 대표적인 Decision Tree 알고리즘에 대해서 알아본다.
인공지능 기술에 대해서 잘 모른다면, 보통 SF 영화에 나오는 로봇들의 이미지를 떠올리면서 막연하게 '기계가 스스로 행동 방식을 정하고 인간처럼 행동하는 것' 정도로 생각할 수 있다. 실제로 바깥에서 보면 그런 것처럼 보이게 만드는 게 인공지능이긴 하지만, 내부적으로는, 그러니까 이걸 구현해야 하는 개발자의 입장에서 보면 철저하게 '알고리즘적' 이라 할 수 있다.
머신 러닝이 등장하기 전에는 인공지능을 구현하기 위해 규칙 기반 (Rule-based) 의 시스템이 많이 이용되었다. 이런걸 전문가 시스템 (Expert System) 이라고도 하는데, "X라는 조건이 만족되고 Y라는 사건이 발생했을 때 Z를 실행한다" 라던지 "X와 Y라는 조건이 만족되면 A는 B이다" 와 같은 규칙들을 엄청나게 많이 집어넣는 것이다.
근데 이런 규칙 기반 시스템은 많은 한계를 가지고 있다. 일단 사람이 직접 규칙을 넣어줘야 하니까 규칙이 많아지면 번거롭다. 그뿐 아니라 단순 규칙으로는 해결하기 어려운 문제도 많은데, 예를 들어서 사진을 보고 개랑 고양이를 구별해야 하는 문제가 있다고 치자. 개와 고양이를 구별하기 위해서는 생김새를 종합적으로 판단해야 할 뿐 아니라 사진은 많은 양의 픽셀로 이루어져 있기 때문에 사람이 규칙을 하나하나 넣어주기엔 부적절한 문제다.
그래서 등장한게 머신 러닝이다. 머신 러닝에서는 알고리즘에 의해 규칙이 자동으로 만들어지므로 사람이 규칙을 하나하나 넣어줄 필요가 없다. 주로 많이 쓰이는 방법은 통계적인 기법인데, 과거의 데이터를 기반으로 해서 현재 주어진 데이터에 대해 분석하거나 미래를 예측하는 것이다. 규칙 기반 방법과 비교했을 때 규칙을 직접 넣어줄 필요가 없고 더 정교한 문제를 풀 수 있지만, 충분한 데이터가 필요하다는 점이나 알고리즘에 들어가는 파라미터 값을 조정하는데 신경을 써야 한다는 점 등 이쪽도 여전히 단점은 있다.
머신 러닝은 그 학습 방법에 따라 크게 3가지 방법으로 나눈다.
1) 지도 학습 (Supervised Learning)
'X이면 Y이다' 라고 달려있는 데이터를 학습에 사용하는 방법이다. 여기서 X를 Feature (또는 Attribute), Y를 Label (또는 Target) 이라고 하는데 Feature는 출력에 영향을 미치는 속성들을 의미하고 Label은 출력, 결과값이다.

예를 들어서 사람의 키랑 몸무게를 통해 성별을 유추하기 위해서 데이터를 수집했는데 '키=170, 몸무게=66, 성별=여자' 라는 데이터가 있다면 키랑 몸무게가 Feature고 성별이 Label이 된다. 이런 데이터 (Training Data라고 한다) 를 쭉 모아서 알고리즘에 따라 규칙을 만들고, '키=173, 몸무게=69, 성별=??' 와 같은 새로운 데이터가 들어왔을 때 그 규칙에 따라서 성별을 유추하는 것이다 (설명을 위한 예시이며 실제로 써먹기엔 Feature가 너무 적다).
지도 학습에서 주로 다루어지는 문제는 분류 (Classification) 문제와 회귀 (Regression) 문제가 있다. X를 통해서 Y를 결정한다는 컨셉은 같지만 분류 문제는 위의 성별 유추 문제처럼 Label이 불연속적인, 이산적인 (Discrete) 값인 경우이고, 회귀 문제는 Label이 실수처럼 연속적인 값인 경우를 말한다.
2) 비지도 학습 (Un-supervised Learning)
Y 없이 X값만 있는 데이터를 학습에 사용하는 방법이다. 대표적인 문제로 군집화 (Clustering) 문제가 있다. 예를 들어서 2차원 좌표상에 점을 막 뿌려놓으면, 점들 사이의 거리를 통해 점들을 몇 개의 집합으로 묶을 수가 있다. '어떤 위치에 있는 점이 A라는 집합에 속한다' 같은 정보는 없이 그냥 묶었으므로 비지도 학습이라 할 수 있다.
3) 강화 학습 (Reinforcement Learning)
현재 상태 (State) 와 현재 상태에서 취할 수 있는 행동 (Action), 그리고 그 행동을 했을 경우 얻을 수 있는 보상 (Reward) 을 정의하고 보상을 최대화할 수 있는 방향으로 행동을 취할 수 있도록 학습하는 것이라고 한다. 다른 두 방법과는 좀 궤가 다르기도 하고 아직은 좀 생소한 분야라 나도 잘 모른다...
위의 영상은 강화 학습 알고리즘의 일종인 Deep Q-Learning을 벽돌깨기 게임에 적용한 영상이다. 영상 초반에 나오는데, Input으로 넣어주는 것은 게임의 조작방법과 게임의 목표 (Score를 최대한 얻는 것) 뿐이라는 것이 핵심이다. 처음엔 허접하지만 시간이 지나면서 학습이 이루어져 나중에는 TAS급 플레이를 보여주는 것을 확인할 수 있다.
여기서부터는 지도 학습, 그 중에서도 대표적인 문제인 분류 문제를 풀 수 있는 Decision Tree 알고리즘의 원리에 대해서 다뤄본다.
아래 표는 전통적으로 지도 학습을 얘기할 때 항상 예시로 나오는 '날씨 데이터' 이다. 맑음 여부, 온도, 습도, 바람의 양에 따라 그날 테니스 경기가 열릴지 열리지 않을지를 결정하는 문제이다. 그러니까 앞의 4가지가 Feature이고, play 여부가 Label이 된다.

이 데이터 간만에 다시 보니까 생각나는게... 크보에서도 우천취소 결정할때 이런거 좀 썼음 좋겠다. 감독관 멋대로 취소하는 꼬라지 좀 그만 보고 싶다.
풀고자 하는 문제는, 저 데이터셋에 없는 새로운 데이터, 예를 들어
Outlook=Sunny, Temp=Cool, Humidity=High, Wind=Strong
가 들어왔을 때 경기가 열릴지 말지 여부를 결정하는 것이다.
이런 분류 문제를 풀기 위한 여러 알고리즘이 있지만, 가장 기초적이고 설명하기 좋으면서 다른 유용한 여러 알고리즘의 베이스가 되기도 하는 결정 트리 (Decision Tree) 알고리즘으로 이 문제를 풀어보자.
기본적으로 Decision Tree는 저 테이블을 트리 형태로 바꿔놓은 것으로, 아래 그림처럼 데이터의 Feature 값들을 따라가다보면 Label 값이 나오는 식이다.
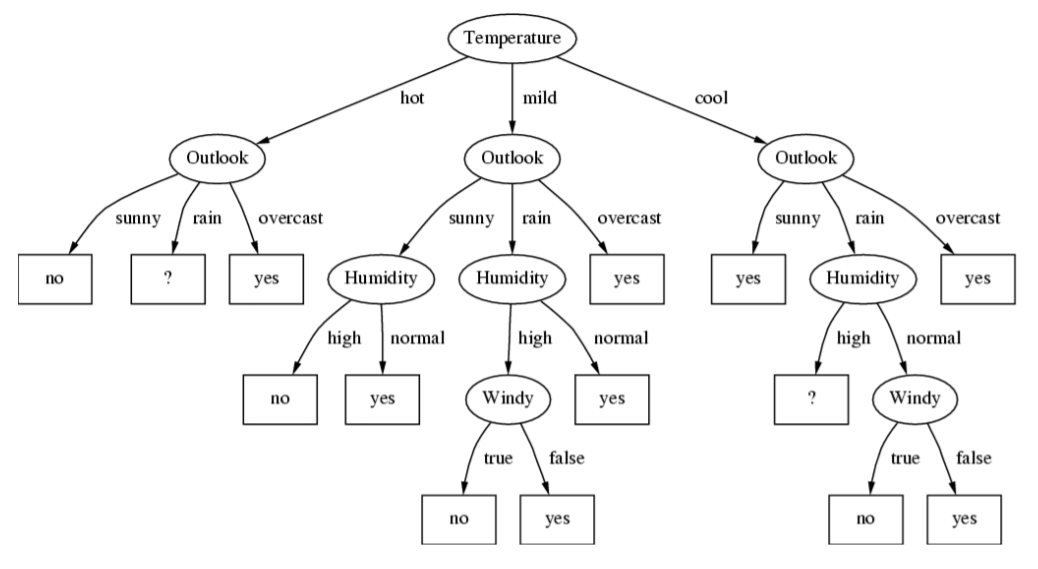
근데 생각해보면 저 테이블을 표현할 수 있는 트리는 이게 유일하지도 않고, 보다보면 뭔가 이상하다. Feature가 들어간 노드가 쓸데없이 중복이 많은 것 같기도 하고, 가지고 있는 Training Data로는 확정할 수 없어서 ?로 남은 박스도 있다. Feature들의 순서가 바뀐 다른 트리도 있을 수 있고, 그 트리가 더 간단하고 정확할 수 있다. 그런데 이게 단순히 여러 개를 넘어서 엄청나게 많기 때문에 (True/False만 존재하는 Feature가 6개만 있어도 그것들로 만들 수 있는 Decision Tree의 경우의 수는 1.8*10^19개나 된다고 한다) 이걸 다 뒤져서 최적의 트리를 찾겠다는 것은 매우 비효율적이다.
더 좋은 Decision Tree를 찾기 위해 쓰이는 아이디어는 트리의 위쪽에 가장 중요한 Feature를 올리는 것이다. 여기서 중요하다는 것은 말로 표현하면 "데이터들이 해당 Feature에 의해서 얼마나 확실하게 갈라지는가?" 라고 할 수 있는데, 이걸 수치적으로 계산하기 위해 엔트로피 (Entropy) 와 정보 이득 (Information Gain) 이라는 개념이 등장한다.
엔트로피라고 하면 일반적으로는 열역학 제2법칙의 그것... 을 떠올리지만 정보&컴퓨터공학 분야에서 엔트로피라는 용어는 '정보의 불확실성' 을 의미한다. 바로 와닿는 개념은 아닌데, 항상 같은 값만 발생한다면 엔트로피가 없는 것이고, 동전 던지기처럼 균등한 확률이 불확실하게 발생한다면 엔트로피가 높은 것이다.
엔트로피를 계산하는 식은 아래와 같다. 여기서 m은 나올 수 있는 Label 값의 집합이며 (yes, no) Pk는 현재 데이터들 중 해당 값이 차지하는 비율을 의미한다. 예를 들어 전체 데이터를 기준으로는 yes가 9개이므로 P(yes)=9/14이다.

모든 데이터가 yes 혹은 모든 데이터가 no라면 엔트로피는 0이고, 데이터가 정확히 yes 반 no 반이라면 엔트로피는 1이다. 그 이외의 경우에는 로그가 들어가는 계산을 해야해서 좀 귀찮다... 공학용 계산기의 도움을 받자.
위의 날씨 데이터의 전체 데이터에 대한 엔트로피를 계산해보자.
- ((9/14) log2 (9/14)) - ((5/14) log2 (5/14)) = 0.94
그 다음 과정으로 각 Feature를 사용해서 데이터를 쪼갠 뒤 엔트로피를 계산한다. 뭔 소리냐면 일단 먼저 Feature로 Outlook을 고른다. Outlook에는 3가지 값이 존재하며 아래 그림과 같이 데이터가 쪼개진다.
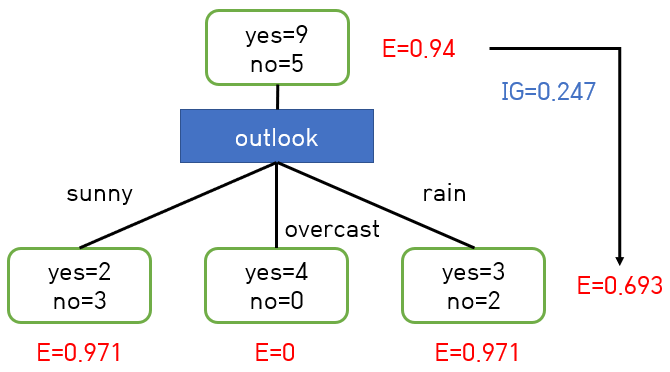
각 자식 노드에 대해서 엔트로피를 계산할 수 있다. 'sunny' 의 경우 yes=2, no=3이다. 엔트로피를 계산하면
- ((2/5) log2 (2/5)) - ((3/5) log2 (3/5)) = 0.971
'overcast' 의 경우 yes=4, no=0으로 한쪽으로만 쏠려있기 때문에 계산해볼 필요도 없이 엔트로피는 0이다.
'rain' 의 경우 yes=3, no=2로 분포가 sunny와 같기 때문에 마찬가지로 0.971이다.
각 자식 노드별로 (데이터 비율 * 엔트로피 값) 을 계산한다.
(5/14 * 0.971) + (4/14 * 0) + (5/14 * 0.971) = 0.693
Feature로 'Outlook' 을 골랐을 때, 다음 레벨의 엔트로피가 0.693이라는 것이다.
이런 식으로 다른 Feature들에 대해서도 다음 레벨의 엔트로피를 구한 다음, 현재 레벨의 엔트로피와 다음 레벨의 엔트로피의 차이를 구한다. 이를 정보 이득 (Information Gain) 이라고 한다. 정보가 불확실하던 상태 (엔트로피가 높음) 에서 정보가 좀 더 확실해진 상태 (엔트로피가 낮음) 로 이동하면서 정보를 얻었다는 의미다.
Feature로 Outlook을 골랐을 때 Information Gain은 0.971 - 0.693 = 0.247이다.
다른 Feature에 대해서도 IG를 계산한 다음, 가장 IG가 높게 나오는 Feature를 이번 레벨에서 데이터를 쪼갤 노드로 선택한다. 이를 반복해나가면서 노드를 만들어내는 것이 Decision Tree 알고리즘이다.
위 그림의 Outlook 자리에 Temp, Humidity, Wind를 넣고 똑같은 방법으로 IG를 계산해보면 Outlook이 IG가 제일 높다는 걸 알 수 있다. 그러므로 Decision Tree의 루트 노드는 Outlook으로 결정한다.
그 다음 단계는 아래 그림과 같을 것이다.

Temp/Humidity/Wind라고 써놓은 건 저 3개의 Feature들에 대해서 각각 위와 같이 IG를 계산하고 제일 높은게 저 자리에 들어간다는 뜻이다.
overcast 쪽으로 내려가면 주황색 상자로 'play=yes' 라고 써놨는데, 저렇게 데이터가 완전하게 한쪽으로 모아진 경우 (즉, 엔트로피가 0인 경우) 에는 더이상 아래에 노드를 추가할 필요가 없으므로 저기서 끝낸다. 저것이 의미하는 것은 outlook=overcast이면 다른 Feature들의 값이 무엇이든 상관없이 무조건 play=yes라는 뜻이다 (데이터 테이블을 잘 보자).

최종적으로 얻을 수 있는 Decision Tree는 위 그림과 같다. 아까 봤던 데이터 테이블에서 아무 데이터나 하나 골라서 이 트리를 따라가보자.
Temp가 분류 기준으로 쓰이지 않았다는 점이 신경쓰일 것이다. 실제로는 아마도 영향을 미치겠지만, 저 Training Data만으로 봤을 때는 Temp가 play 여부를 결정하는데 영향을 미치지 못하고 있다.
이렇게 구축한 트리에 의해서 처음에 봤던 문제의 답을 내보자.
Outlook=Sunny, Temp=Cool, Humidity=High, Wind=Strong
트리를 따라가보면 분류 결과는 play=no이다. outlook=sunny -> humidity=high이기 때문이다.
그 외에 Decision Tree나 분류 문제에 대한 추가적인 이슈들을 써보면 이런 것들이 있다. 이쪽으로 더 자세히 배우진 못해서 아는 만큼만 짤막하게 쓴다.
- Overfitting & Generalization
과적합 (Overfitting) 현상이란 Decision Tree 뿐 아니라 머신 러닝 분야에서 광범위하게 사용되는 표현으로, 학습 모델이 Training Data에 지나치게 딱 맞게 만들어지다보니 너무 복잡해지고 학습 시간이 오래 걸리는 현상을 말한다. 뿐만 아니라 일부 튀는 데이터 (noise/outlier) 가 있는 경우에도 그 데이터에까지 맞추려고 하다보니 정확도마저 떨어지는 경우도 있다.
이런 현상을 완화시켜주는 것이 Generalization인데, Generalize를 하게 되면 모델이 단순해지고 학습 시간이 적게 걸리는 대신 정확도가 떨어질 수도 있다.
- Pruning
'가지치기' 라는 뜻이며 위에서 설명한 Generalization 기법에 속한다. 이미 엔트로피를 기준으로 제대로 나눴는데 왜 또 가지를 치느냐고 할 수 있는데, 이렇게 하고도 트리에 너무 가지가 많을 수도 있고, 위의 알고리즘을 잘 보면 사실 greedy 알고리즘이라 (Information Gain이 당장 제일 큰 것부터 고른다) 완벽하지는 않다는 것이다.
일반적으로 아래 레벨로 내려갔는데 데이터의 yes-no 비율이 변하지 않는다면 의미 없는 가지로 본다 (Null Hypothesis). 관련된 방법으로 chi-square pruning이라는 게 있다고 한다.
- Numeric Input Feature
Label 말고 Feature 중에서 값이 연속적인 숫자인 경우가 있을 수 있다. 예를 들어서 위의 날씨 데이터에서 Humidity가 High/Normal이 아니라 정수값으로 주어진다고 치자. 이 상태로 그대로 트리를 만들면? 값 하나하나마다 가지를 치면 트리가 무지막지하게 커질 것이다. 그러므로 이런 경우엔 적당한 경계값을 정해서 High/Normal/Low 같이 묶어주는 것이 좋다. 경계값을 정할 때는 그 경계를 기준으로 Label의 분포가 확 바뀌는 지점, 즉 이렇게 나누면 Information Gain이 제일 커지겠다 싶은 지점으로 정하면 좋다.
- Missing Data
언제나 Training Data Set이 완벽하면 좋겠지만 실제로 데이터를 수집하다보면 그렇지 않은 경우가 많다. 데이터를 표로 만들어보면 중간중간에 구멍이 숭숭 뚫려있곤 하는데, 이런 Missing Data를 처리하는 방법이 필요하다. 간단하게 생각할 수 있는 방법으로는 다른 적당한 값 (다른 데이터들의 평균값 등) 으로 채워넣는 방법도 있고, Training 때는 다른 Training Data들의 분포에 따라 해당 데이터를 소숫점 단위로 쪼개서 처리하는 방법을 쓸 수도 있다. 즉 yes=60.6개 / no=39.4개 같은 식의 분포가 나올 수 있다.
- 모델의 검증: k-fold Cross Validation & Confusion Matrix
Decision Tree를 만들었다고 그걸 아무런 검증 없이 바로 실제 시스템에 넣을 수는 없다. 이렇게 만들어진 Decision Tree가 데이터를 얼마나 정확하게 분류하는지 테스트해볼 필요가 있는데, 이 때 주로 쓰이는 방법이 k-fold Cross Validation이라는 것이다.
교차검증 (Cross Validation) 은 현재 가지고 있는 데이터를 쪼개서 일부는 Training Set으로, 일부는 Test Set (예측해야 할 대상 데이터 역할) 으로 쓰는 것을 의미한다. 예를 들어서 원래 Training Set의 데이터가 300개면 그 중에 200개는 Training Set으로, 나머지 100개는 Test Set으로 쓴다.
이걸 Test Set을 바꿔가면서 k번 실행하면 k-fold가 된다. 3-fold Cross Validation이라면 첫 테스트는 1~100번째 데이터를 Test Set 나머지를 Training Set, 두번째 테스트는 101~200번째 데이터를 Test Set, 마지막 테스트는 201~300번째 데이터를 Test Set으로 쓰는 것이다.

분류기의 성능을 평가하는 지표 (Metric) 로는 Accuracy, Precision, Recall이 널리 쓰이는데, 위 그림과 같은 Confusion Matrix를 참고해서 구할 수 있다.
Accuracy가 우리가 흔히 얘기하는 정확도이다. 그러니까 yes를 yes라고 분류하고 (True Positive) no를 no라고 분류한 (True Negative) 비율이다. 위 그림에서는 총 270개 데이터 중에 200개가 제대로 분류되었으므로 20/27이 된다.
Precision은 yes라고 예측한 것 (Predicted Positive) 중에 yes가 맞은 경우 (True Positive) 의 비율로, 위 그림에서는 100/120 즉 5/6이 된다.
Recall은 실제 데이터의 값이 yes인 것 (Actual Positive) 중에서 yes로 제대로 예측한 경우 (True Positive) 의 비율로, 위 그림에서는 100/150 즉 2/3이다.
이외에 F1 Score (Precision과 Recall의 조화평균) 같은 지표도 있다.
- Ensemble Learning
앙상블 기법이란 여러 개의 학습 모델을 돌려서 합치는 기법을 말하는데, Decision Tree를 이용한 앙상블 알고리즘도 있다. Decision Tree 여러개에다가 각각 weight를 주고, 학습시키면서 Error Rate에 따라 weight를 조절해주는 Boosted Tree라는게 있고, Random Forest라는 알고리즘도 Decision Tree를 기반으로 하는 유명한 학습 알고리즘이다.