Intro. 왜 Java 8인가? Java 8 (=Java 1.8) 은 2014년에 발표된 자바 버전이다. 내가 대학에서 자바를 배웠던 것은 Java 8이 발표되기 전이었다. 당연히 Java 8의 신기능에 대해서 대학 수업에서는 배우지 못했다 (조금 더 늦게 자바 수업을 들었다고 해도 배울 수 있었을지는 알 수 없지만). 학교 수업 이외에 개발 공부를 별도로 하고 있지 않았던 나로서는 대학을 졸업할 때까지 Java 8 버전을 쓰면서도 Java 8이라는 얘기를 딱히 들어본 적이 없었다. 졸업하고 한참 시간이 지나 부트캠프에서 개발을 다시 배우게 되었다. 커리큘럼 중에 Java 8의 추가기능에 대해 배우는 파트가 있었다. 이 포스팅에서 소개할 Lambda 식, Stream API, Functional Int..
2020/05/09 Codeforces 첫 도전 - Round #640 Div. 4
Codeforces는 외국 알고리즘 저지 사이트로, 백준처럼 각종 알고리즘 문제를 풀어볼 수 있을 뿐 아니라 주기적으로 대회를 개최하는 걸로 유명한 사이트다. 대회에서 거둔 성적에 따라 레이팅을 얻을 수 있어서, 알고리즘 문제풀이를 즐기는 사람들 사이에선 코드포스 레이팅으로 실력을 가늠하기도 한다... 고 하더라. 나는 딱히 알고리즘 문제풀이가 취미인 사람은 아니고 그냥 취준 하다보니 백준이랑 SWEA 들락거리면서 지금 다니는 곳에서 내주는 과제 정도나 푸는 사람이다. 더구나 내가 알고있던 정보는, 코드포스 대회는 Div. 1이랑 Div. 2 두 개의 부문이 있는데 둘 중에 낮은 레벨인 Div. 2만 해도 3번 문제부터는 백준 solved.ac 기준으로 골드 상위에서 플티 이상급 문제가 튀어나오는 굉장히..
[BOJ] 다리 만들기 2
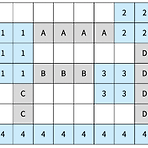
https://www.acmicpc.net/problem/17472 17472번: 다리 만들기 2 첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다. www.acmicpc.net 삼성 역량테스트 A형 (= 삼성 SW직군 공채 코딩테스트 수준) 기출 문제. 위 그림과 같은 맵이 주어지고, 파란색을 섬이라고 한다. 모든 섬을 연결할 수 있도록 다리 (회색) 를 놓아야 하는데 다리의 총 길이가 최소가 되도록 놓았을 때 그 길이를 구하는 문제이다. > 다리는 가로 or 세로, 일직선으로만 놓아야 한다 > 두 섬을 잇기 위해 다리를 놓았는데 중간에 또다른 섬이..